Rule:
start with $1, and keep betting the same until you lose. When this occurs, double the size of bet for the next spin. This way, in case you win, you will recover the money you lost on the previous round, and win something extra. If keeping on losing, keep on doubling your bet. As soon as you win, you should restart and bet $1 for the next spin.
Summary of parameters
| parameter | description | starting value |
|---|---|---|
| B | Starting budget | $200 |
| W | Winnings threshold for stopping | $300 (Starting budget + $100 winnings) |
| L | Time threshold for stopping | 1000 plays |
| M | Casino’s maximum wager | $100 |
library(dplyr)
library(tidyverse)
#' A single play of the Martingale strategy
#'
#' Takes a state list, spins the roulette wheel, returns the state list with updated values (for example, budget, plays, etc)
#' @param state A list with the following entries:
#' B number, the budget
#' W number, the budget threshold for successfully stoping
#' L number, the maximum number of plays
#' M number, the casino wager limit
#' plays integer, the number of plays executed
#' previous_wager number, the wager in the previous play (0 at first play)
#' previous_win TRUE/FALSE, indicator if the previous play was a win (TRUE at first play)
#' @return The updated state list
one_play <- function(state){
# Wager
proposed_wager <- ifelse(state$previous_win, 1, 2*state$previous_wager)
wager <- min(proposed_wager, state$M, state$B)
# Spin of the wheel
red <- rbinom(1,1,18/38)
# Update state
state$plays <- state$plays + 1
state$previous_wager <- wager
if(red){
# WIN
state$B <- state$B + wager
state$previous_win <- TRUE
}else{
# LOSE
state$B <- state$B - wager
state$previous_win <- FALSE
}
state
}
#' Stopping rule
#'
#' Takes the state list and determines if the gambler has to stop
#' @param state A list. See one_play
#' @return TRUE/FALSE
stop_play <- function(state){
if(state$B <= 0) return(TRUE)
# the player goes bankrupt
if(state$plays >= state$L) return(TRUE)
# the player completes L plays
if(state$B >= state$W) return(TRUE)
# the player gets to the budget threshold for successfully stoping
FALSE
}
#'
#' @param B number, the starting budget
#' @param W number, the budget threshold for successfully stoping
#' @param L number, the maximum number of plays
#' @param M number, the casino wager limit
#' @return A vector of budget values calculated after each play.
one_series <- function(
B = 200
, W = 300
, L = 1000
, M = 100
){
# initial state
state <- list(
B = B
, W = W
, L = L
, M = M
, plays = 0
, previous_wager = 0
, previous_win = TRUE
)
# vector to store budget over series of plays
budget <- rep(NA, L)
# For loop of plays
for(i in 1:L){
new_state <- state %>% one_play
budget[i] <- new_state$B
if(new_state %>% stop_play){
return(budget[1:i])
}
state <- new_state
}
budget
}
# helper function
get_last <- function(x) x[length(x)]
The codes above simulates a series of roulette plays that continue until
the player budget drops to zero (the player has lost all their money)
the player has reached winning threshold of $300
the casino play limit is reached
Possible Outcome
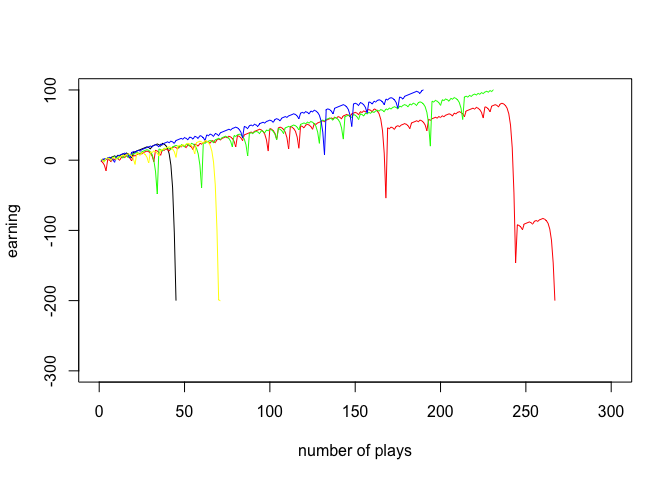
There are different patterns for the game. One may soon lose all his money(black line), he may win a lot at the first beginning and suddenly lose all his moeny(red line) and he may also keep on winning and get 100 earning(blue & green line).
Simulation
Let’s repeat the process for 10000 times to determine the performance for Martingale’ Strategy.
#Simulation
walk_out_money <- rep(NA, 10000)
for(j in seq_along(walk_out_money)){
walk_out_money[j] <- one_series(B = 200, W = 300, L = 1000, M = 100) %>% get_last
}
# Walk out money distribution
hist(walk_out_money, breaks = 100,xlab="walk-out money",main='histogram for 1000 simulations')
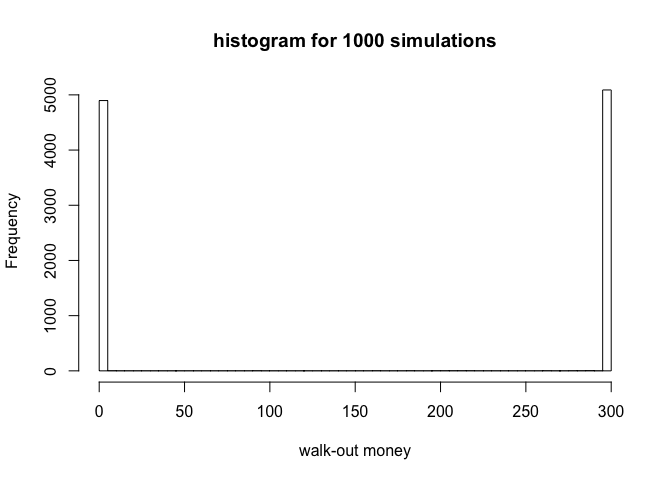
We could see that about half of the time that the player will lose all his money and half of the time that the player will reach the winning threshold of $300. There is no 1000-plays before either going broke or reaching the winning threshold of $300).
# Estimated probability of walking out with extra cash
mean(walk_out_money > 200)
## [1] 0.5098
# Estimated earnings
mean(walk_out_money - 200)
## [1] -47.0411
The probability that the player will win money is 50.98%. Additionally, the average earning for the simulation is -47.0411. Thus, the Martingale strategy actually resulted in an average loss.
Change Starting Budget
Let’s set the starting budget B to be 50 to 300 and calculate the average earning for 1000 simulations
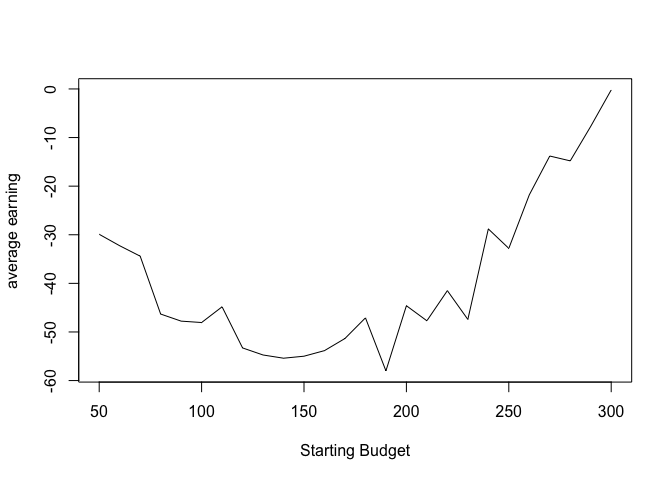 For budget in range (50,300), the average earning will decrease at first and then increase.
For budget in range (50,300), the average earning will decrease at first and then increase.
Change Winnings Threshold
Let’s set the winnings threshold W to be 250 to 350 and calculate the average earning for 1000 simulations.
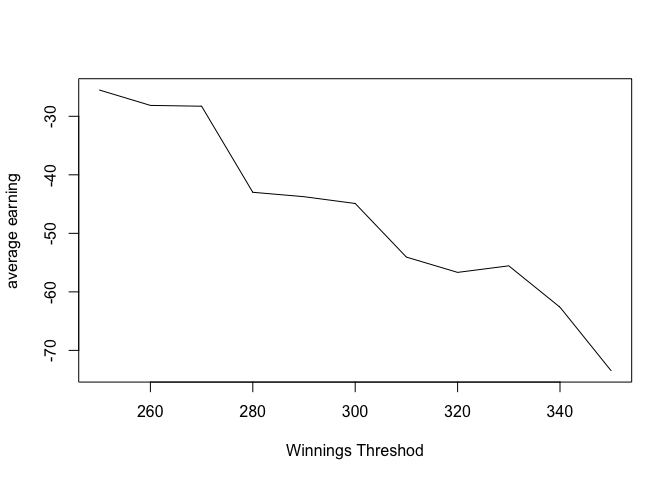 For winnings threshold in range (250,350), there is a decreasing trend for average earning. As people get more greedy, it is very possible that they will end up losing more moeny.
For winnings threshold in range (250,350), there is a decreasing trend for average earning. As people get more greedy, it is very possible that they will end up losing more moeny.
Change Time Threshold for Stopping
Let’s set the time threshold for stopping to be 10 to 300 and calculate the average earning for 1000 simulations.
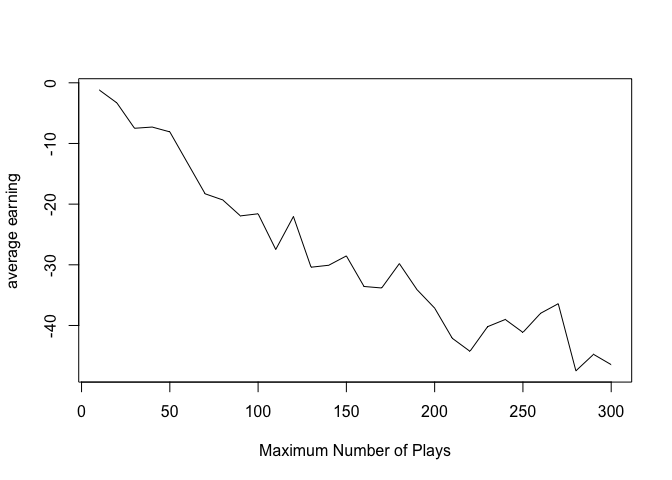 Since the average number of plays is around 200, I set the L in range(10,300) and there is a decreasing trend for average earning.
Since the average number of plays is around 200, I set the L in range(10,300) and there is a decreasing trend for average earning.
Change Casino’s Maximum Wager
Let’s set the Casino’s maximum wager to be 50 to 300 and calculate the average earning for 1000 simulations.
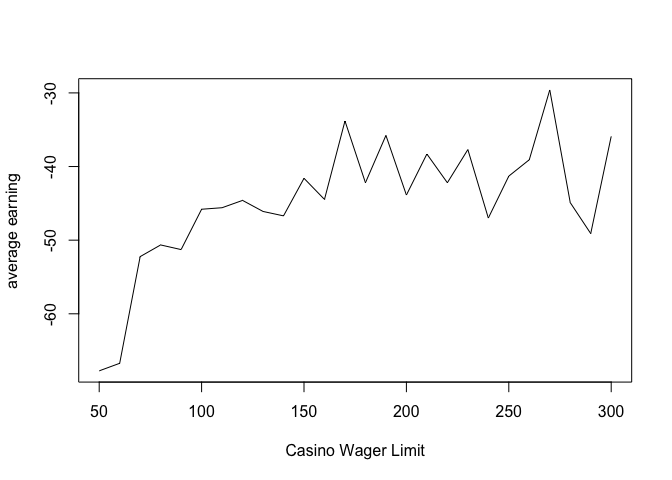 For Casino Wager Limit in range (50,300), there is an increasing trend at first, after 100, there is no obvious pattern about how casino wager limit would affect average earning. After this point, the casino wager limit may not be an important factor to stop the game.
For Casino Wager Limit in range (50,300), there is an increasing trend at first, after 100, there is no obvious pattern about how casino wager limit would affect average earning. After this point, the casino wager limit may not be an important factor to stop the game.
Average Number of Plays
## [1] 200.8133
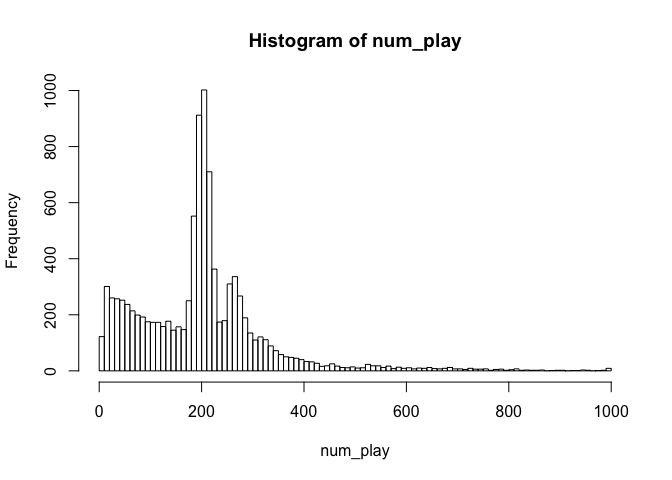
The average number of plays is around 200. For 10000 simulations, most of the number of plays would fall into the range (0,400)
Limitation & Simplification
The simulation involves a computer with higher memory and processor speed.
For budget threshold, it may change during the play. For example,if one win a lot of money over several plays, he may not want to stop at 300 since people are greedy. Since the house will always end up winning eventually, the casino may not set a certain wager limit for play.