The World Series is the annual championship series of Major League Baseball (MLB) in North America. The winner of the World Series championship is determined through a best-of-seven playoff, and the winning team is awarded the Commissioner’s Trophy.

Suppose that the Braves and the Yankees are teams competing in the World Series
Best-of-7 Match-up
Rule:out of 7 sets, the team which wins 4 sets out of 7, wins the game
| What is the probability that the Braves win the World Series given that PB=0.55? |
| Team | The probability that the team win in any given game |
|---|---|
| the Braves | PB=0.55 |
| the Yankees | PY=1-PB=0.45 |
For best-of-7 match-up, the Braves could win the series in 4,5,6 or 7 games
For a team to win the series in game N, they must have won exactly 3 of the first N-1 games and won the last game
| win the series in game N | situation | probability |
|---|---|---|
| 4 | 3 wins in 3 & win last game | dnbinom(0,4,0.55) |
| 5 | 3 wins in 4 & win last game | dnbinom(1,4,0.55) |
| 6 | 3 wins in 5 & win last game | dnbinom(2,4,0.55) |
| 7 | 3 wins in 6 & win last game | dnbinom(3,4,0.55) |
pnbinom(3,4,0.55)
## [1] 0.6082878
Now we want to know the probability that the Braves win the World Series given a series of PB
| What is the probability that the Braves win the World Series given that PB=x? |
| Team | The probability that the team win in any given game |
|---|---|
| the Braves | PB=p |
| the Yankees | PY=1-PB=1-p |
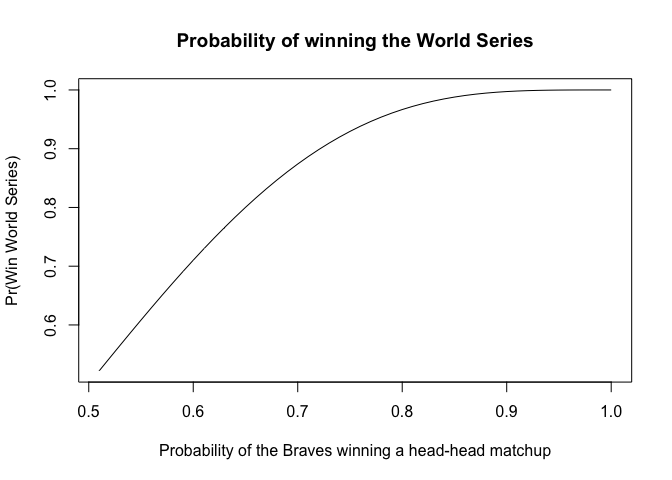
This is the figure (see below) with PB on the x-axis and P(Braves win World Series) on the y-axis. As PB increases, the probability that the Braves win the World Series will also increase
get_probability <-function(p){
pnbinom(3,4,p)
}
plot(x=seq(0.51,1,0.01),y=get_probability(seq(0.51,1,0.01)),xlab='Probability of the Braves winning a head-head matchup',ylab='Pr(Win World Series)',main="Probability of winning the World Series",type="l")
Best-of-N Match-up
Suppose one could change the World Series to be best-of-9 or some other best-of-X series
Rule:out of N sets, the team which wins (N+1)/2 sets out of N, wins the game
| What is the shortest series length so that P(Braves win World Series\|PB=0.55)≥0.8 |
# define a function to calculate the probability of win world series given best-of-N series and PB
get_probability <-function(N,p){
pnbinom((N-1)/2,(N+1)/2,p)
}
# use for loop to get the shortest series length
for (i in seq(1,999,2)){
if (get_probability(i,0.55)>=0.8){
print(i)
break
}
else next
}
## [1] 71
Under the assumption PB = 0.55, the shortest series length is 71 so that Braves have at least 80% chance to win World Series
Shortest Series Length
Given a series of PB, we want to know the shortest series length so that Braves have at least 80% chance to win World Series
| What is the shortest series length so that P(Braves win World Series\|PB=x)≥0.8 |
This is the figure (see below) with PBon the x-axis and shortest series length is the y-axis.
# create an empty vector with length 500
c=rep(NA,500)
# run simulation
for (i in 1:500){
for (j in seq(1,999,2)){
if (get_probability(j,0.5+0.001*i)>=0.8){
c[i]=j
break
}
}
}
plot(x=seq(0.501,1,0.001),y=c,xlab='Probability of the Braves winning a head-head matchup',ylab='shortest series length',main="Shortest series so that P(Win WS given p)≥0.8",type="l")
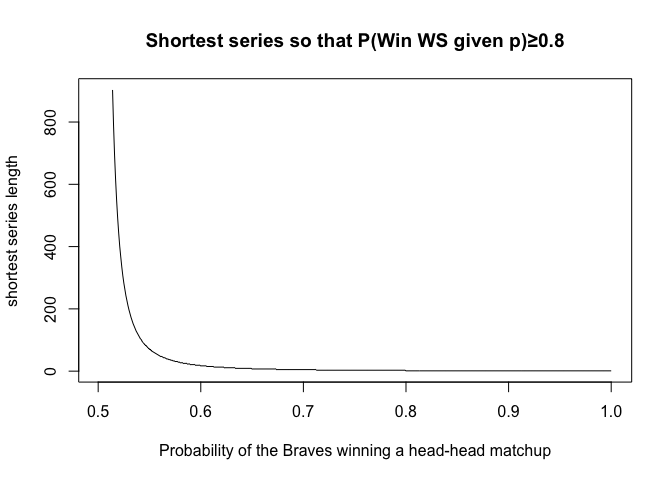
You may notice, as PB increases, the shortest series length decreases
Best-of-7 Match-up (win 4 lose 3)
Let’s go back to best of 7 series, suppose Braves lose 3 games before winning a 4th game
The prior probability would be:
| assumption | probability |
|---|---|
| PB=0.55 | 0.5 |
| PB=0.45 | 0.5 |
| Calculate P(PB=0.55|Braves win World Series in 7 games) under the assumption that either PB=0.55 or PB=0.45 |
apply the Bayes’ rule here

dnbinom(3,4,0.55)*0.5/(dnbinom(3,4,0.55)*0.5+dnbinom(3,4,0.45)*0.5)
## [1] 0.55